How Finalyse can help
The highest possible predictive power of your models
Model Validation: are you sure your internal risk parameter estimates are adequate, robust and reliable?
Control your model risk with the right tool to develop and validate models, bridge the talent gap and reduce implementation risks
Reviewed by Can Soypak
Introduction
The accurate estimation of the credit risk parameters is critical for precise assessment of provisioning (IFRS 9) and capital requirements (IRB) as well as for setting up strategies for pricing, risk appetite setting, etc. However, this task can be especially challenging in portfolios with limited or no defaults, as statistical models that rely on an adequate number of defaults may not be as reliable in predicting and managing risk in low-default environments. Consequently, alternative methods and data sources may be needed to ensure accurate risk estimation.
Low default portfolios (LDPs) are characterised by low number of historical defaulted observation clustering in specific downturn periods, and low-risk obligors. Low default likelihood can be observed in different portfolios, such as sovereigns, typically characterized by low default rates due to the rarity of past defaults by countries. Other examples of low-default portfolios include banks, insurance companies, and individual bank-level project finance.
Fortunately, there are multiple methods available when modelling these portfolios. However, the challenge lies in the absence of a single best practice approach; the suitability of any modelling approach depends on various factors such as the portfolio characteristics, segment, data availability, rating homogeneity, etc. Therefore, the application of any alternative modelling technique for LDPs must be evaluated for each case. This blog post aims to elaborate on the relevant regulatory landscape as well as the challenges and potential solutions for dealing with the LDPs.
Regulatory Requirements
The LDPs appeared in the regulatory context for the first time in the 'International Convergence of Capital Measurement and Capital Standards,' also known as Basel II (June 2004). Later, another paper was published by Basel in 2005 focusing on the validation techniques for the LDPs ('Validation of low-default portfolios in the Basel II Framework'). These papers recommended that LDPs should not be excluded from the IRB scope without justification and that alternative modelling/calibration techniques shall be investigated for LDPs.
In 2013, the 'Analysis of risk-weighted assets for credit risk in the banking book' was published. During the same year Prudential Regulation Authority was established with (among others) the aim to standardize the definition for the low default portfolios and sets the threshold for low default portfolios at 20 defaults per rating system.
More recently, in April 2021, the European Central Bank (ECB) released the Targeted Review of Internal Models (TRIM) to evaluate banks' internal credit risk models. Regarding LDPs, TRIM aims to confirm that banks possess adequate models for assessing and controlling the credit risk associated with their investments. This report examines the data quality of the models in use, the calibration methods applied, and the overall strength, stability and accuracy of the LDP credit risk models.
Moreover, regulators recognize banks' challenges in implementing IRB models for LDPs and have provided various options and alternatives to ease the modelling burden for LDPs. For instance, some banks have transitioned from advanced-IRB (A-IRB) to foundation-IRB (F-IRB) as a result of modelling difficulties in estimating risk parameters loss-given default (LGD) and exposure at default (EAD) for LDPs. Meanwhile, other banks have adopted Supervisory Slotting Criteria, which are guidelines used by regulators to determine the risk weights for specialised lending portfolios that are typically characterised by low default nature. Notably, this method differs from traditional approaches and does not require any calibration for PD or LGD parameters.
Why do we apply different treatments to LDPs?
Different approaches should be explored for LDPs to avoid producing statistically unreliable and volatile results instead of employing conventional credit risk modelling methodologies. The limited number of default events complicates drawing meaningful conclusions about the default probabilities/loss amounts and underlying risk factors particularly for rare or extreme events that may not represent the accurate distribution. Additionally, standard approaches such as the maximum likelihood estimation used for the PD modelling (i.e., logistic regressions) can be affected by small-sample bias.
Challenges
It's widely recognized that Low Default Portfolios are a challenging subject. However, it's worth exploring the most complex aspects and modelling steps associated with LDP modelling. This chapter will therefore focus on the target definition, sampling, and calibration approaches for LDPs.
Target Definition - Extended Default Definition
The Extended Default Definition examines the appropriate methodology for assigning probabilities of default (PD) or loss-given default (LGD) that would allow the modellers to have a more balanced sample in terms of the distribution of good vs. bad customers (for PD modelling) or to increase the sample size (for LGD/CCF modelling). However, it is mandatory for regulated banks to follow the internal default definition for the calibration of IRB models, although there is flexibility in choosing an alternative target definition for model development (ranking) purposes.
To address the issue of low defaults in a portfolio the natural option is to increase the number of defaults. This can be achieved through two methods. The first method is to extend the default observation window beyond 12 months while also ensuring that the selected time horizon is appropriate for the general characteristics of the portfolio. The second method is to expand the default trigger by using a DPD of 60, 30 or 10 days instead of 90 DPD as a default indicator. Although this approach is expected to increase the number of defaults, there is still a possibility that the number of defaults may not be sufficient for modelling.
Sampling
In order to comply with the Basel requirements, IRB models for PD/LGD/CCF must be developed based on long-run average realised 1-year default rates (PD calibration), realised loss rates (LGD calibration) or realised conversion rates (CCF calibration).
Oversampling and Undersampling
Oversampling or undersampling1 can be employed as sampling alternatives for LDPs, with the goal to increase the ratio of defaults/bads in the development sample using methods such as bootstrapping. In oversampling, the objective is to increase the number of defaults/bads, while in undersampling, the aim is to reduce the number of non-defaults/goods. This technique is used on the training dataset, and it is essential to maintain a close approximation to the original class distribution to prevent significant distortion of the statistics due to biased probabilities. Different methods such as stratified sampling can be employed to avoid any representativeness issues caused by oversampling or undersampling.
Footnote 1 There are two commonly used sampling methods. Stratified sampling - dividing population into homogeneous subgroups and selecting samples from each subgroup for full representation. Random sampling - selecting samples randomly to ensure equal representation of the entire population. |
Artificial oversampling via SMOTE
Another sampling approach for LDP modelling is to create synthetic/artificial observations. The aim is to create synthetic observations based on the existing defaulted observations, rather than simply increasing the number of default events. For LDPs, we can consider non-defaulters as the majority and defaults as the minority. In this approach, k-nearest neighbours are calculated for these minority records. The magnitude of oversampling is critical here, and the number of k-nearest neighbours to choose from is determined accordingly. Assuming that neighbours are randomly selected, the goal is to generate synthetic samples by randomly selecting values between these neighbours.
Next, a synthetic example is generated for one or more of the sample's characteristics by selecting a random value between 0 and 1. This synthetic oversampling and undersampling approach is combined for both the majority and minority classes and is referred to as SMOTE. In the original paper written by Chawla(2002), it was observed that the SMOTE method works better than simple undersampling or oversampling techniques.
Calibration approaches
Another challenge for LDP modelling is calibration. When examining the calibration approaches applied to Low Default portfolios, it is helpful to make two distinctions: the first is to decide whether the default events are
- dependent or,
- independent
and the second is to know whether the portfolio has
- no defaults or,
- a limited number defaults
Pluto and Tasche
The Pluto and Tasche method can be applied to both dependent and independent default events. This method is also applicable for portfolios with no defaults.
This method was developed to provide a conservative estimate of independent defaults for a single period (i.e, no cross-sectional or intertemporal correlation). For illustration purposes, the reader can assume a scenario where there are three rating grades: A, B, and C, with A being superior to B and B being superior to C.
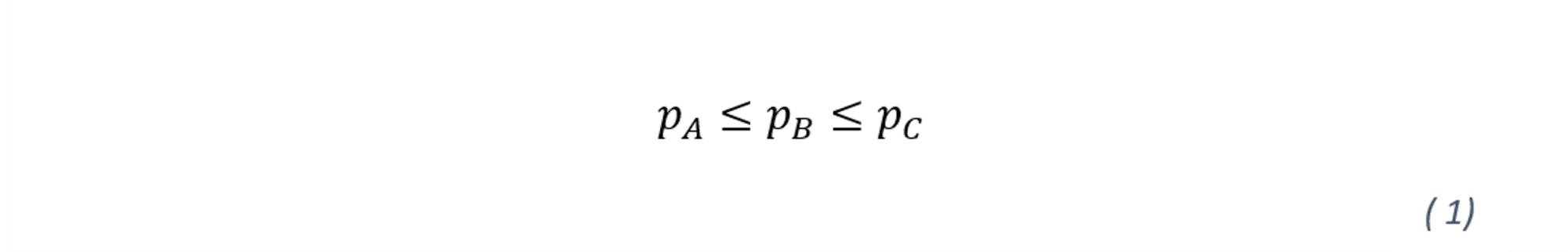
First, all rating grades are assumed to have the same credit quality.
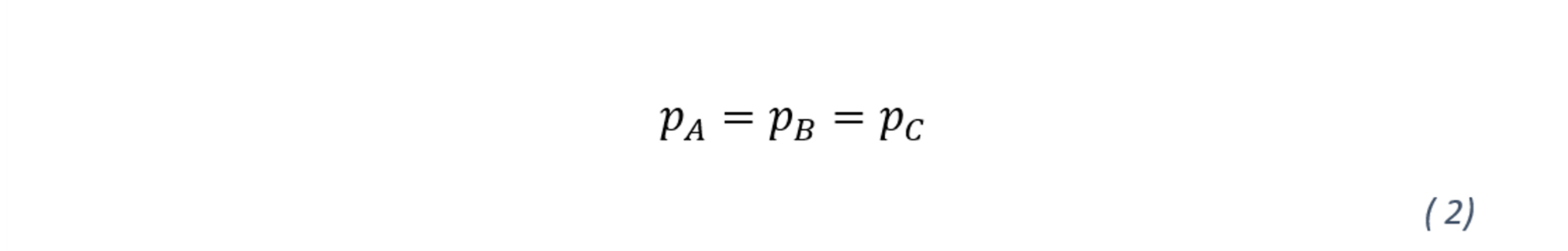
A confidence interval is defined for the distribution of the probability of default for all these rating grades. The upper confidence interval should not include the rejected values (p-value>𝛼), which is determined by the significance level 𝛼 associated with the confidence level 𝛾 through the equation 1 - 𝛾 = 𝛼.
According to the most prudent principle, the p-value estimate should be based on all borrowers in the portfolio. Thus, the most prudent principle implies the estimate of the best rating class should be based on all the obligors and all the defaults. The variable 𝑘 denotes the observed defaults, whereas n represents the number of debtors in each rating. The PD confidence levels of each rating grade (i) are computed by defining a subsample which consists of the observation from the respective rating grade as well as the observations from worse rating grades. Hence, the most prudent estimator for pA is obtained by solving the equation, where kA+=kA+kB+kC and nA+nB+nC :
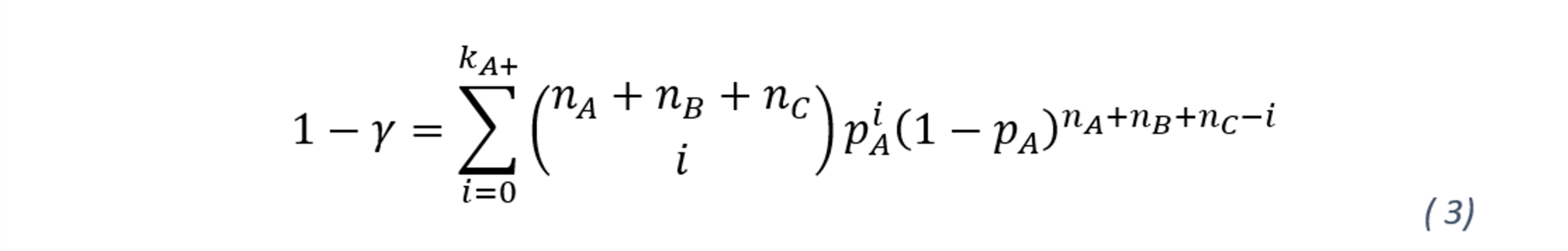
Hence, PD estimates for the best rating grade (A) is defined based on the full sample. In terms of rating scales, using pA as an upper bound of pB would not be the most prudent estimation, as it is established that pB is higher or equal to pA . Therefore, to determine the most prudent estimator for pB at a given upper confidence level 𝛾, the following equation needs to be estimated:
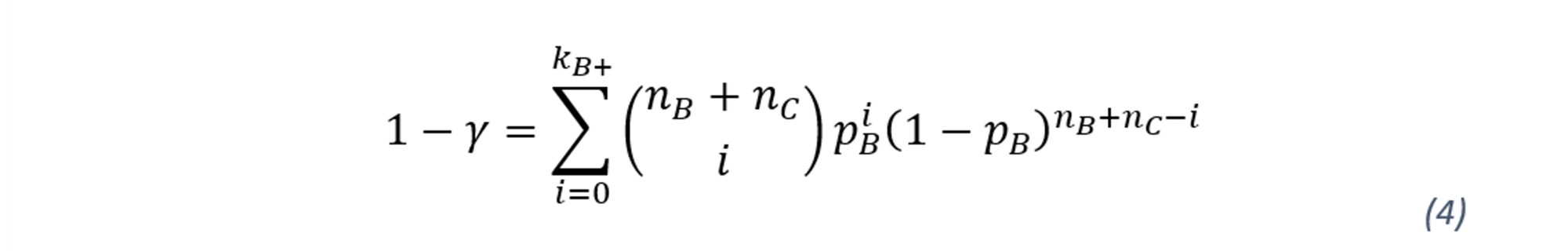
In other words, the observations from rating grade A are eliminated leaving only B and C in the sample for the estimation of PD for rating grade B. In that logic, pC does not have any upper bounds as which the worst rating grade. Thus, the most prudent of pC is simply the solution of the following equation:
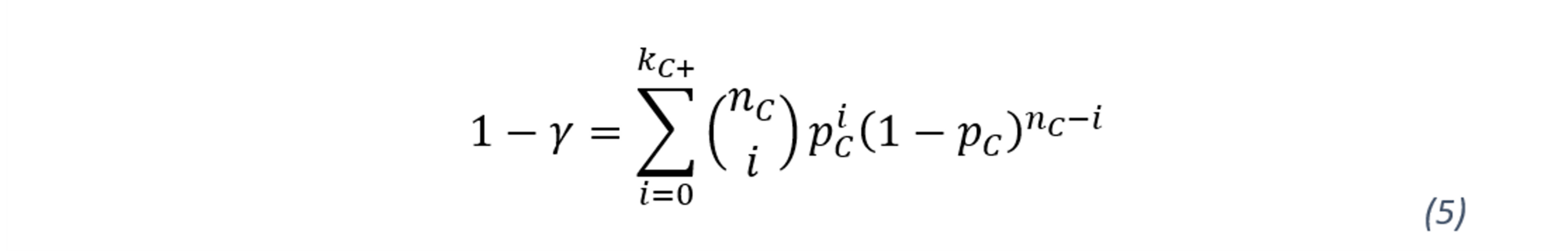
On the downside of this method, setting the confidence interval level can be critical, since a higher confidence interval generates a more conservative estimate. Moreover, Pluto and Tasche method is only applicable to PD, not to LGD and EAD estimations.
The original Pluto-Tasche methodology (as described in Equations 3-5 above) assumes cross-sectional and intertemporal independence of the default events to derive the PD estimates. However, this assumption can be modified, and cross-sectional dependence of the default events can be introduced using a one-factor model containing systemic risk. Similarly, their intertemporal correlation generated by the dependence structure of the systemic risk factors over time. Introducing these correlation structures, the cross-sectional and intertemporal correlation between default events will be taken into consideration.
Quasi Moment Matching (QMM)
Originally Quasi Moment Matching is designed as another calibration approach for PDs in LDPs, where model scores (rankings) are calibrated to estimated PDs using a simple equation. The approach requires two inputs: target accuracy ratio and the mean portfolio PD (central tendency). This creates two-dimensional nonlinear equation that can be solved using numerical methods.
Standard two-parameter approach can be described as
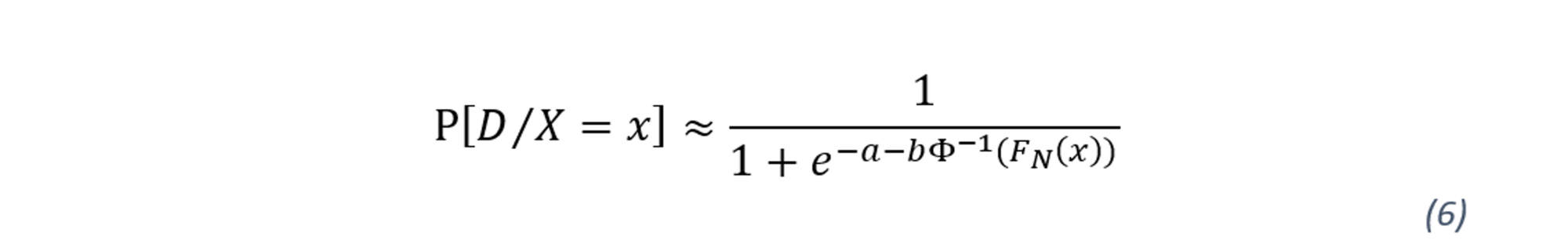
where FN(x) is the empirical cumulative distribution function of the rating grades conditional on survival (i.e., observations were not in default in the performance period). Note that this function results from transformation of the non-parametric distribution of the ratings to an approximately normal distribution.
Numerical solution of parameters of a and b is initialised by assuming a binormal model with equal variances between the defaulted and non-defaulted classes. Binormal model in a nutshell is based on two states; defaulted or non-defaulted and it assumes distribution where default ~ Nμ>0,1 and non-defaulted ~ N(0,1) . Solving for conditional densities of continuous scores of borrowers in case of default and no default, will provide the estimated parameters for the two parameters of a and b in the function above. Inserting these estimated parameters into the equation above will in turn produce the calibrated PDs. Tasche (2013) provides a detailed explanation as well as insights with respect to the details of QMM methodology.
Alternatively, QMM parameters can also be estimated using a logistic regression of the target variable (i.e., default flag) on the model scores/rankings. This logistic regression approximates the original QMM method quite accurately also allowing QMM to be used for LGD/EAD calibration, even though it is primarily designed for PD models. For instance, for low-default LGD calibration, QMM can be implemented where logistic regression method is replaced with fractional logistic regression to estimate the parameters of a and b .
Bayesian Methods
In the context of parameter estimation, Bayesian methods and frequentist methods (i.e Pluto-Tasche, classical fractional logistic regression etc) differ in the sense that Bayesian methods treat parameters as random variables. On the other hand, frequentist approaches derive point estimates using maximum likelihood estimation (MLE), whereas Bayesian methods estimate the central tendency posterior probability conditional on priors by leveraging on MAP (maximum a-posteriori method) which maximizes the posterior distribution. Eventually, MAP provides a point estimation such as mode or mean of the posterior distribution.
As in the frequentist approaches, Bayesian methods use the same statistical model structure, yet they allow to embedding the prior information (can be informative and non-informative) of the independent variables into the estimation process. A-priori information might include the probability distribution of intercept and initial values of the coefficients of risk drivers. Consequently, a generative model of an assumed distribution with parameters of the model, is simulated. After, obtaining the generative model, with risk data and priors; it is possible to obtain posterior distribution of the parameters by using MCMC (Markov Chain Monte Carlo) methods such as Metropolis, Gibbs, Hamiltonian, etc.
One advantage of using Bayesian methods in the context of LDPs is that it eliminates the need for selecting confidence intervals. In frequentist approaches, parameters are fixed but the confidence intervals are random variables, whereas in Bayesian methods, parameters are random variables and confidence bounds are fixed. With priors, if a parameter has a subjective probability that its posterior distribution lies between certain values, then these values become the confidence bounds. Another advantage is that expert opinion can be incorporated through informative priors, which can help to better address the unique features of the portfolio. In this way, the LDP transformation is less agnostic to portfolio-specific issues. Lastly, Bayesian methods can be easily adapted to accommodate correlation structures between default events.
Programming Packages
Various software packages can be used to implement Pluto-Tasche, QMM and/or Bayesian calibration methods.
| Pluto-Tasche | R | PTMultiPeriodPD |
| Python | GitHub - LDP | |
| SAS | Customized code required | |
| QMM | R | LDPD |
| Python | GitHub - vdb | |
| SAS | Customized code required | |
| Bayesian | R | Bayeslm, rstanarm, brms |
| Python | pymc3, pyro | |
| SAS | PROC MCMC |
Although Matlab does not have specific packages for these approaches, all these methods can also be easily implemented with MATLAB’s Toolbox.
Conclusion
Due to their unique characteristics, Low Default Portfolios pose distinct challenges that require modellers to explore different modelling and calibration approaches as explained above. The adjustments of target definition, sampling techniques and calibration approaches are essential for effectively managing LDPs.
This article has not only highlighted the latest developments related to credit risk modelling in the realm of LDPs, but also demonstrated how Finalyse can be a key player in exploring and implementing the state-of-the art modelling solutions for LDP.
With its demonstrated experience in credit risk modelling, the Finalyse Risk Advisory team can provide seasoned consultants to develop the approaches highlighted in this article, and tailor them to the needs and specificities of your institution.
Finalyse InsuranceFinalyse offers specialized consulting for insurance and pension sectors, focusing on risk management, actuarial modeling, and regulatory compliance. Their services include Solvency II support, IFRS 17 implementation, and climate risk assessments, ensuring robust frameworks and regulatory alignment for institutions. |

Our Insurance Services
Check out Finalyse Insurance services list that could help your business.
Our Insurance Leaders
Get to know the people behind our services, feel free to ask them any questions.
Client Cases
Read Finalyse client cases regarding our insurance service offer.
Insurance blog articles
Read Finalyse blog articles regarding our insurance service offer.
Trending Services
BMA Regulations
Designed to meet regulatory and strategic requirements of the Actuarial and Risk department
Solvency II
Designed to meet regulatory and strategic requirements of the Actuarial and Risk department.
Outsourced Function Services
Designed to provide cost-efficient and independent assurance to insurance and reinsurance undertakings
Finalyse BankingFinalyse leverages 35+ years of banking expertise to guide you through regulatory challenges with tailored risk solutions. |

Trending Services
AI Fairness Assessment
Designed to help your Risk Management (Validation/AI Team) department in complying with EU AI Act regulatory requirements
CRR3 Validation Toolkit
A tool for banks to validate the implementation of RWA calculations and be better prepared for CRR3 in 2025
FRTB
In 2025, FRTB will become the European norm for Pillar I market risk. Enhanced reporting requirements will also kick in at the start of the year. Are you on track?
Finalyse ValuationValuing complex products is both costly and demanding, requiring quality data, advanced models, and expert support. Finalyse Valuation Services are tailored to client needs, ensuring transparency and ongoing collaboration. Our experts analyse and reconcile counterparty prices to explain and document any differences. |

Trending Services
Independent valuation of OTC and structured products
Helping clients to reconcile price disputes
Value at Risk (VaR) Calculation Service
Save time reviewing the reports instead of producing them yourself
EMIR and SFTR Reporting Services
Helping institutions to cope with reporting-related requirements
Finalyse PublicationsDiscover Finalyse writings, written for you by our experienced consultants, read whitepapers, our RegBrief and blog articles to stay ahead of the trends in the Banking, Insurance and Managed Services world |

Blog
Finalyse’s take on risk-mitigation techniques and the regulatory requirements that they address
Regulatory Brief
A regularly updated catalogue of key financial policy changes, focusing on risk management, reporting, governance, accounting, and trading
Materials
Read Finalyse whitepapers and research materials on trending subjects
Latest Blog Articles
Contents of a Recovery Plan: What European Insurers Can Learn From the Irish Experience (Part 2 of 2)
Contents of a Recovery Plan: What European Insurers Can Learn From the Irish Experience (Part 1 of 2)
Rethinking 'Risk-Free': Managing the Hidden Risks in Long- and Short-Term Insurance Liabilities
About FinalyseOur aim is to support our clients incorporating changes and innovations in valuation, risk and compliance. We share the ambition to contribute to a sustainable and resilient financial system. Facing these extraordinary challenges is what drives us every day. |

Finalyse CareersUnlock your potential with Finalyse: as risk management pioneers with over 35 years of experience, we provide advisory services and empower clients in making informed decisions. Our mission is to support them in adapting to changes and innovations, contributing to a sustainable and resilient financial system. |

Our Team
Get to know our diverse and multicultural teams, committed to bring new ideas
Why Finalyse
We combine growing fintech expertise, ownership, and a passion for tailored solutions to make a real impact
Career Path
Discover our three business lines and the expert teams delivering smart, reliable support




