How Finalyse can help
The impairment model will impact investment decisions and create additional challenges in your accounting, modelling and reporting functions
The highest possible predictive power of your models
Model Validation: are you sure your internal risk parameter estimates are adequate, robust and reliable?
Written by Prashant Dimri, Consultant.
Introduction
This paper discusses the Z-score methodology, a robust framework for estimating the Probability of Default (PD) at portfolio and pool levels, aligning with IFRS 9 standards. IFRS 9 introduces a structured framework for estimating expected credit losses (ECL) across three stages: Stage 1 (1-year ECL), and Stages 2 and 3 (lifetime ECL). Z-score methodology calculates worst-case default rates (WCDR) based on asset correlation (ρ), market factor (Z), and threshold (k) values using the Vasicek formula. This paper explores the range of applications for the Z-score methodology at portfolio and pool levels, while also discussing various methods for calculating asset correlation used in the Vasicek formula.
Z-score methodology
Portfolio level
At the Portfolio-level, the assessment begins with the calculation of worst-case default rates (WCDR) using the Vasicek formula, a widely accepted approach in financial risk modelling. This formula requires the inputs such as asset correlation (ρ), market factor (Z), and threshold (k) values to derive WCDRs, which serve as foundational metrics in assessing credit risk. The main trick for an appropriate Z-score methodology implementation is the estimation of the asset correlation (ρ) and there are multiple methods that can be utilized for this purpose:
1. Indirect moment approach: The Vasicek formula for point in time (PiT) PD estimation is defined as
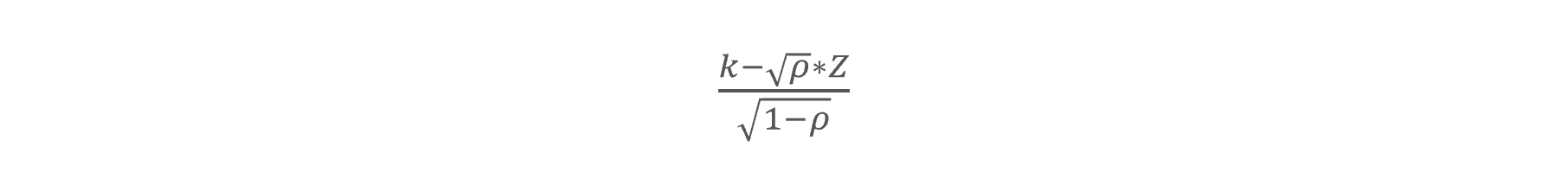
which is derived from the one factor copula model with the equation
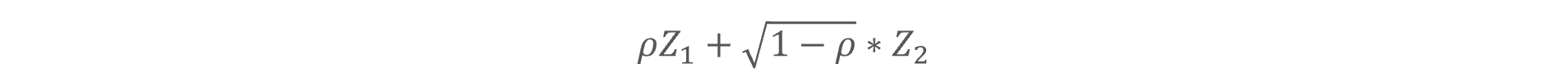
where Z1 and Z2 represent the systematic and idiosyncratic factors, respectively. As the market factor in the Vasicek equation is assumed to follow the standard normal distribution, the mean, and the standard deviation of it is equal to 0 and 1 respectively, thus the mean for PiT PD will be equal to
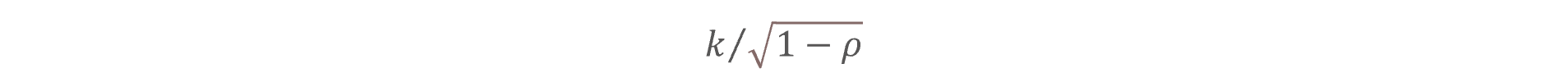
and the standard deviation is equal to
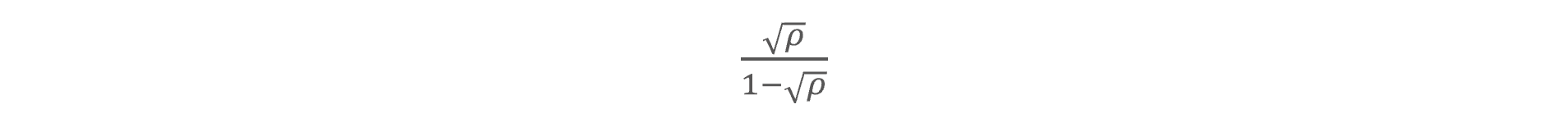
These two equations can be solved to derive the correlation and threshold (k).
2. Direct moment approach: In this approach, the first (m1) and second moments (m2) of default rates are used, which are the expected values such as m1 = E(X), m2 = E(X)2, and so on, to estimate the correlation coefficient (ρ) between default events of different assets. This correlation coefficient tells us how intricately linked these default events are. The equation of this is given by
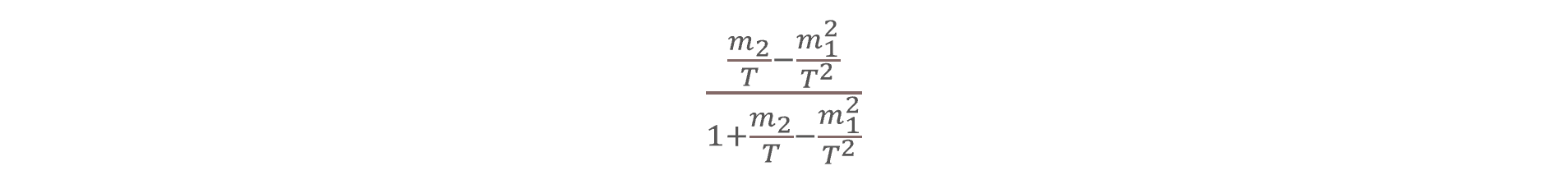
where T is the total number of observations. Next, the likelihood function is being used to make sense of these moments and estimate ρ more precisely. This equation calculates the likelihood of observing the default rates given a certain correlation coefficient (ρ) and default probability (p) i.e., quantifying how well the model fits the observed data. The likelihood equation is given by
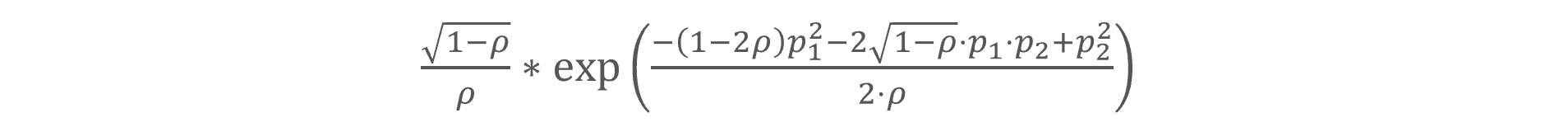
where p1 and p2 are the observed default frequency and the PD respectively, and where the PD is calculated as
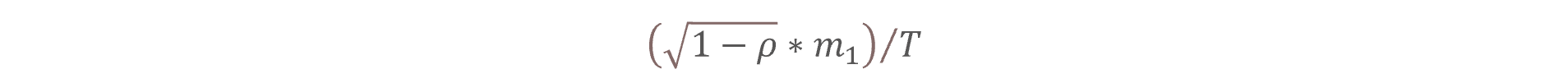
By adjusting the correlation coefficient (ρ) and the default probability (p), we try to maximize the likelihood of our observed data. This optimization process helps us find the best-fitting values for correlation (ρ) and default probability (p).
3. Vasicek probability density function: Another approach to modelling probabilities is the Vasicek density function. This function is derived using the formula
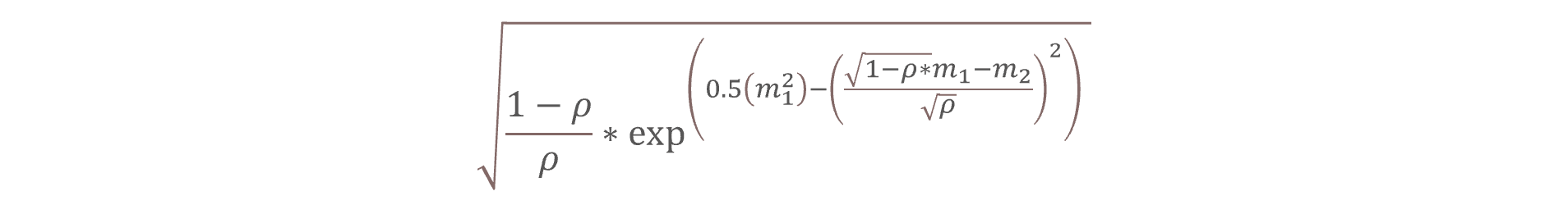
where the density is calculated based on the observed and the average default rates, denoted as m1 and m2 respectively in the formula. In this, the parameter correlation (ρ) represents an optimization parameter, adjusted to maximize the sum of log-likelihoods.
Consequently, the market factor (Z) is calculated as
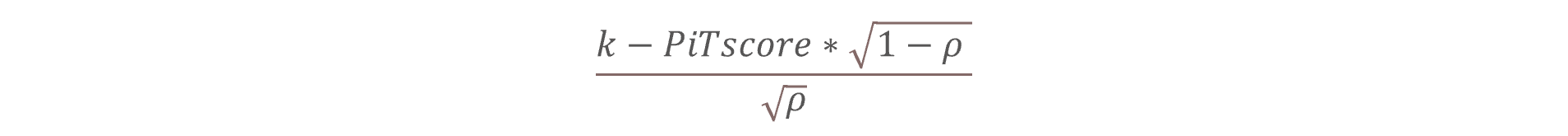
where PiT score is the inverse standard normal distribution of default rates. Hence, it can be said that the WCDR is transformed into Z-scores, representing the PiT market factor. These Z-scores capture deviations from the mean default rate and provide insights into the relative creditworthiness of the portfolio. Through regression analysis with the macroeconomic variables, such as GDP growth, interest rates, unemployment rates, etc., these Z-scores can be forecasted, thus giving forecasted unconditional PDs eventually for different years. This regression analysis enables financial institutions to model the impact of economic fluctuations on credit risk and anticipate potential shifts in default probabilities over time (see ‘A PRACTICAL APPROACH TO PREDICTING THE IFRS9 MACROECONOMIC FORWARD-LOOKING PD”.)
Pool level
Conversely, at the pool/rating grade level, the Z-score methodology requires deciphering transition probabilities between different states, such as S1, S2, and S3. These transition probabilities reflect the likelihood of borrowers transitioning between credit states over a specified time horizon. By leveraging historical data and optimization techniques, financial institutions can calibrate these transition probabilities to current market conditions and future economic outlooks. The culmination of these analyses is the estimation of marginal PiT PDs, which encapsulate the projected default probabilities for each period within the loan lifecycle.
Consider the example Table1 below, where migration probabilities are defined for transitions between credit stages, such as from S1 to S1, S2, and S3. These probabilities illustrate the likelihood of borrowers moving between credit states and let us say these are TTC (through the cycle) or average transitional probabilities.
To understand the distribution of probabilities across various stages, a probability distribution graph is constructed as below (Graph1). This graph provides insights into the relative frequencies of transitions.
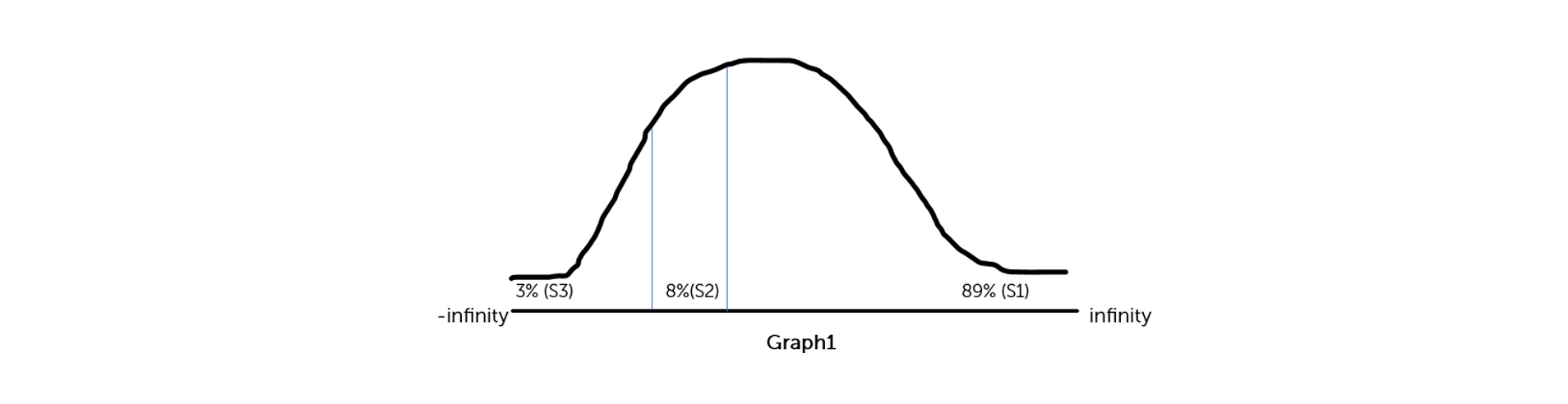
Using the provided probabilities, the upper and lower bounds are calculated as thresholds in the Vasicek formula. So, these thresholds (k) along with correlation (ρ) and market factor (Z) yield the worst-case PiT PD matrix which can be termed as fitted migration matrix herein. In short, TTC PD will get transformed into PiT PD with this formula.
Using an optimization engine such as Solver, Z and ρ are recalibrated in such a manner that the difference between actual PiT migration matrix and fitted migration matrix is minimized. This same exercise can be done for different years with different correlation values, and as such, this will yield the specific Z value for each year and eventually yield the time-series of Z.
This is an iterative process which can be done using VBA (Visual basic) or any other programming language. The other condition for this optimization problem is that ρ (correlation) should be calibrated to ensure that the variance of the Z series equals 1. Once the Z-series are established, they are regressed against macroeconomic variables to forecast future Z values. These Z forecasts, along with the upper and lower bounds and the ρ value, inform the calculation of transitional probabilities for various stages.
To adapt the methodology for pool-level modelling, adjustments might be needed for additional states such as write-off. Hence, the transitional probability table should be modified to ensure normalization, i.e., a sum of each row equal to 100%. The example below with Table2 shows 3 distinct stages (1, 2 and 3) along with the write-off stage. The migration from S1 to S1, S2 and S3 for different forecasted years can be seen. For Stage 3 accounts, write-off is considered as well.
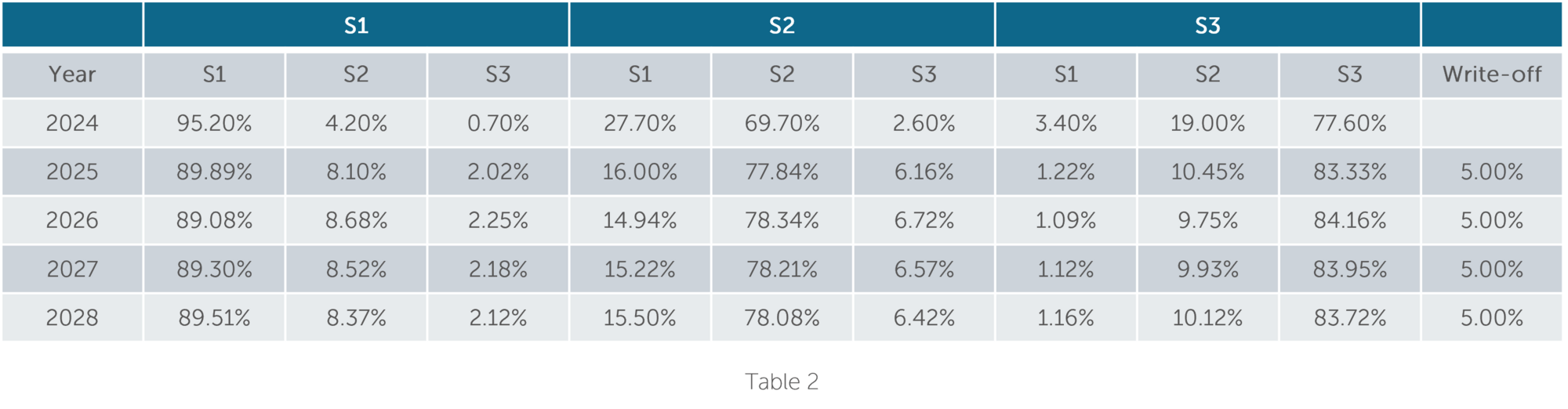
The derived conditional PDs for the 3 distinct stages from the migration matrix are then converted into unconditional PDs. This step is essential for incorporating PDs into the final Expected Credit Loss (ECL) calculation. While migration probabilities are commonly used for the pool level PD estimations, there are different granularity levels in practice for the definition of pools/segments (e.g., Days Past Due (DPD) buckets, ratings, etc.) (See: IMF working paper).
Conclusion
The Z-score methodology provides a comprehensive framework for estimating the Probability of Default (PD) at both portfolio and pool levels, offering alignment with IFRS 9 standards. By leveraging the Vasicek formula, financial institutions can derive worst-case default rates (WCDR) and transform them into Z-scores for forecasting marginal PDs through regression analysis with macroeconomic variables. This approach not only facilitates accurate portfolio-level credit risk assessments but also optimizes transition probabilities at the pool level to derive marginal PiT PDs. Furthermore, through various methods for calculating asset correlation, the Z-score methodology enhances the precision of credit risk modelling, supporting robust and forward-looking ECL estimations as required by IFRS 9.