About Callable Bonds
In this blog post, we introduce the pricing of callable bonds using interest rate models. In our work across Derivatives Model Validation, Market Risk and IRRBB framework implementations, we frequently encounter material positions in callable bonds within client portfolios. The embedded optionality of these instruments adds significant complexity to their valuation and risk assessment compared with standard bonds. This overview offers practical guidance for modelling and managing that complexity.
We begin by explaining the principles behind pricing callable bonds, followed by an introduction to interest rate models, with a focus on the Hull-White one-factor model. We then demonstrate how to calibrate the model and use it to price a callable bond. Based on the resulting price and sensitivities, we highlight key characteristics of callable bonds. Finally, we discuss their treatment under IRRBB and FRTB regulatory frameworks.
For further reading on Market Risk, FRTB and IRRBB, you can refer to our blog posts on the latest reporting requirements for FRTB, our article about the IMA approach and methods to calculate Value-at-Risk and Expected Shortfall, our blogpost about IRRBB management, as well as our article on Non-Maturity Deposit modelling techniques.
Callable bond’s pricing and sensitivities calculations
How to price a callable bond
A callable bond is a bond that can be reimbursed anticipatively by the issuer on a unilateral basis, for example when cheaper funding sources are available on the market. For pricing purposes, a callable bond can be considered as the combination of a plain bond and a call option (a cap) sold to the issuer (callable bond = plain bond + short option). One approach is to first calculate the option value using an analytical Black-76 model. This approach works well in cases where the bond is callable on a single date. But generally, there is a call schedule, for example yearly call dates starting 5 years after issuance. The bonds may also be callable continuously after the first call date. In both cases, the option’s expiry is of a non-European type (respectively Bermudian or American) and hence the options cannot be priced analytically. Although, the Black-76 model may be used as an approximation, more rigorous pricing requires the use of a numerical approach (trees, lattices, finite-difference methods or Monte Carlo simulations).
Interest rate models and their usage in calculating callable bond’s price
A bond’s price is dependent on the current yield curve, which has a risk-free and a credit or liquidity risk spread component (also known as z-spread). In this article, we follow the industry practice of modeling the bond call option using an interest rate model, assuming that the credit/liquidity spread is constant (non-stochastic). To price an option, we then need to define the probability distribution of the yield curve and the payoff of the option.
There are numerous models to model the interest rate movements, but the more common and straightforward approach is to model the instantaneous short rate. The forward rates and the yield curve are then implied from the drift (or trend), volatility and possibly mean reversion parameters assigned to the short rate. A consequence of this approach is that the different tenors of the yield curve are fully correlated to the short rate movement. This is acceptable for the pricing of bond options. Indeed, an analysis of yield curve movements using a Principal Component Analysis, shows that most of the movements across the term structure (~85%) can be explained by a single factor associated to changes in the level of the yield curve (i.e. parallel shifts)1. Obviously, by modelling only the short rate, we cannot model changes in the yield curve shape (e.g., twists in the yield curve). For options where the payoff depends on the curvature or slope of the curve (e.g., CMS spread options), generally a 2-factor model is used.
In its most basic form, a short-rate model specifies the evolution of the short rate with an equation of the following form:
dr=b (r,t) dt+σ (r,t)dz
Changes in the short rate (dr) depend on:
- a drift term (br,t ), which may follow a time structure and depend itself on the level of the short rate (r), introducing a mean-reversion effect;
- the volatility of the short rate (σ), which may be dependent on time and the level of the short rate.;
- a random “white noise” process, typically a Weiner process (normal distribution with a mean of zero and a standard deviation of one).
The initial suite of interest rate models – like Vasicek and CIR models were able to provide closed form solution for pricing zero-coup bonds (ZCB) and European-style options, but they lacked the ability to match the current yield curve. Such models where the term structure of interest rates is produced endogenously (“inside the model”) are called “equilibrium models”. In contrast, “no-arbitrage models” allow for the term structure of interest rates to be provided as an input as part of the drift term. Example of these are the Hull-White and the Black-Karasinski model.
Hull-white one-factor model (HW1F)
In this article we are using the HW1F model to price callable bonds. The reason for choosing this model is its ubiquity and the fact that it gives analytical formulations for the price of many interest rate options like caps, floors and swaptions. The analytical formulas allow for the calibration of the model parameters against market prices, as these vanilla options are quoted on the market. Calibrated parameters can then be used in numerical simulations to price more complex option payoffs. The model also has desirable features - It can capture the (empirically observed) mean-reverting behavior of interest rates and fit the initial yield curve accurately. Importantly, the model also accommodates negative interest rates, making it suitable in low or negative rate environments.
Assumptions
- Short rate is normally distributed and consequently the ZCB prices are log-normally distributed
- The short rate follows a Ornstein–Uhlenbeck (OU) process, i.e., a mean reverting random walk process
- The pricing of the bond is done in a risk-neutral probability setting, i.e., considering no arbitrage
Specification
- Stochastic Differential Equation (SDE) for short rate
- drt = [θ(t) − αrt] dt + σ dZt
Properties
- The function θ(t) is a term-structure paramater that is selected so that the model fits the initial term structureof interest rates
- The parameters α (mean-reversion) and σ (volatility) are calibrated to fit the current market prices of a set of actively traded interest rate options (more on this below)
Calibration
- The general realtionship between the price of zero-coupon bonds (P) and forward rates is as follows:
- Using the above relationship and ito's lemma for OU process, we can derive the below formulated value for "theta". The α and σ parameters are taken as an assumption and then calibrated in the last steps.
- As a next step, a useful property of the HW1F model is that the (log of) ZCB prices can be formulated as a linear function of the short rate, using a so-called "afine term structure" (ATS) as follows:
The values for functions A and B are not provided here for brevity. This is a powerful simplification, as ZCB prices usually depend on the complete set of forward rates until final redemption.
- The ATS representation then allows for the derivation of closed form solutions for European options on ZCBs and the so-called "Jamshidian decomposition" is used to treat European swaption as a sum of European options on ZCBs.
- Finally, the resulting closed-form solution for swaptions is used to calibrate model parameters (α and σ) against publicly available market quotes.
How to price the Call Option
In this article we assume that the callable bonds have an American exercise type and develop a trinomial tree or lattice approach to pricing. A trinomial tree is used to construct a discrete time approximation of the SDE for short rate.
In this approach, the entire price evolution is modelled as a tree of possible paths branching out and recombining, where at each discrete time step, the short rate can move to 3 possible states (up/down/stay the same). The probabilities are chosen so that the tree matches the drift and variance of the HW1F process, under the calibrated parameters.
Below is a high level illustration of the trinomial branching process. On X-axis is the future time, the Y-axis (j) signifies the change in short rate and each node represents the various states that the short rate can be in. From each node there is a positive probability of an up, down or no move. The probabilities are a function of α, j and change in time.
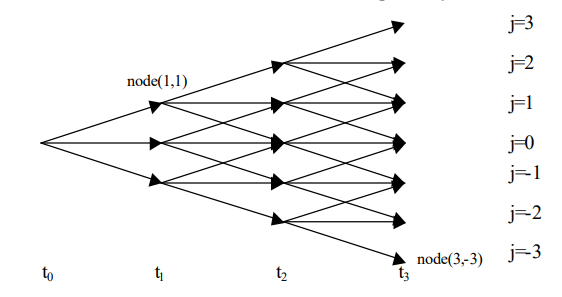
Once the tree is built, the bond price and option payoff are first valued at every node of the tree. Then the option is priced by working backwards in the tree: at each node the option value equals the discounted risk-neutral expectation of the three successor node values - unless early exercise applies, in which case the maximum of exercise and continuation is taken.
Implementation of the above steps (Quantlib and Finalyse’s internal pricers)
We worked through a short example, starting with the calibration of a Hull-White 1 factor model using Quantlib, an open-source pricing library. Post-calibration, we calculated the price of the bond and option and compared it with market quote. The calculation was also benchmarked against Finalyse’s internal pricing engine (Finalyse Valuation Services). The steps are summarized below:

Observations and properties of the callable bond
We priced a listed Bond (ISIN: FR001400F067, CCY: EUR, Value date: 20/06/25, Close price: 107.05, Rate type: Fixed) which has a callable date 3.25 years from the value date and maturity at 3.75 years from the value date.
The Bond was rated as BBB and hence a credit spread was applicable on the Bond. Before calculating the θ(t) parameter, the credit spread applicable on the Bond should be added yield curve. Since this was a Callable Bond, the Option Adjusted Spread (OAS) was calculated. OAS is similar to the Z-spread (as defined earlier), but adjusted for the option price:
The OAS can be calculated by using an interest rate model (like HW1F) by first calibrating it and then calculating the OAS using the market price of the Bond. For this exercise we used a similar approach by calibrating the HW1F model and then using the quoted price of the Bond and the HW1F tree approach, the OAS was calculated by recursively updating the spread component. Another (approximate) approach to calculate OAS is to use the market quoted Z-spread for similar rating and tenure of the Bond, although this approximation will not replicate the exact price of the Callable Bond.
Next, the OAS was added to the yield curve and this updated curve was used for the HW1F calibration and subsequently for the Callable Bond valuation.
Below are some plots which showcase the price of the callable bond, the option price, and the bond price without the option (stripped bond), with respect to various interest rate shocks. We see that the option price increases as the interest rates reduce and consequently the difference between the callable bond price and the stripped bond price increases. Intuitively, as rates decline, the issuer is able to access cheaper alternative funding and has a greater incentive to redeem the bond early.
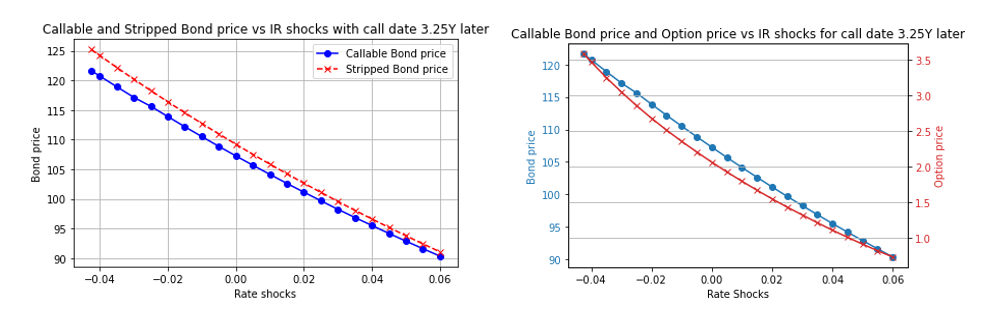
However, in this example, the value of the call option is limited because the first call date is only 6 months before the final bond redemption and the benefits from calling the bond are limited. In order to understand dynamics of the callable bond pricing, we keep the bond maturity unchanged but reduce the first call date from 3.25 years to 1.25 years from value date. The results are displayed in the new plots below. As expected, due to the higher residual maturity of the bond on the first call date, the option price has increased and its sensitivity to interest rate shocks has also increased.
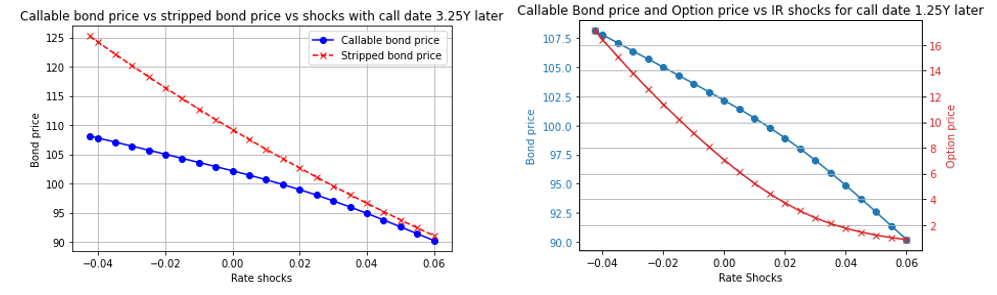
A comparison of the bond price and option price with respect to the 2 different residual maturities is presented below. We see that as the rates become higher (i.e., chances of call option being exercised becomes lower), the price of both options converges. Concurrently, the price of the 2 callable bonds are very different in a negative shock scenario and converges when the shocks are high.
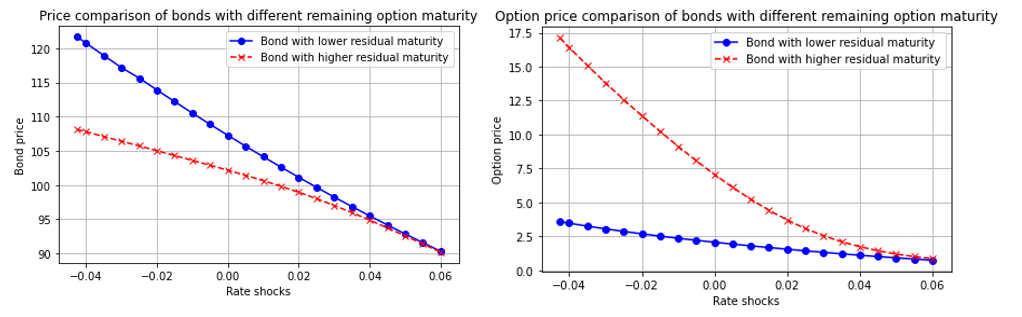
Finally, to illustrate the impact of callability on a bond’s duration and convexity, we plotted below the duration of 3 bonds against a range of interest rate shocks. The first bond (blue) is a plain bond with a maturity of 1.25Y from value date. In effect, this is the representation of a bond callable after 1.25Y when a bank assumes that the bond will be called immediately 100% of the time. The second bond (red) is a callable bond with the first call date in 1.25Y and final maturity in 3.75Y using our HW1F model. The third bond (green) is the actual bond quoted in the market (i.e., callable “lately” after 3.25Y and maturing after 3.75Y), again priced using our HW1F model.
We see that the duration of the bond callable after 1.25Y with a final maturity after 3.75Y (red) is very sensitive to interest rate movements (high convexity). When rates are low, callability is certain and its duration converges to the duration of the plain bond with a maturity of 1.25Y (green). As interest rate increases, the gap with the plain bond increases and the duration eventually converges towards the bond that is callable “lately” (green). We also see that the duration of the bonds with no or very “late” callability (blue, green) declines slightly as interest rates increase, while the duration of the bond with a high option value (red) shows an opposing trend.
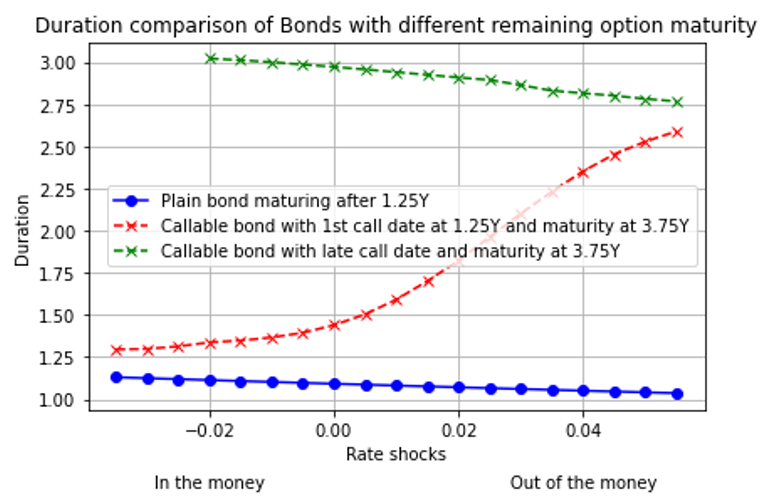
These observation illustrate the importance of modelling callability correctly and the severe limitations of assuming that callable bonds always repay on the first or next call date.
IRRBB treatment of Callable Bonds
Under the Basel III guidelines (or variations thereof under local jurisdictions), as part of Pillar 2 requirements, banks need to assess the Interest Rate Risk in the Banking Book (IRRBB) by calculating key metrics such as the change in Economic Value of Equity (ΔEVE) and Net Interest Income (ΔNII).
The cashflow slotting for IRRBB purpose for a callable (fixed rate) bond issued by a bank can be done in two ways. The first approach (recommended) is to slot the principal of the bond based on the final maturity date and then treating the call option as an automatic interest rate option. The second option is to slot the principal based on the expected duration taking the bond’s optionality into account. As illustrated by our analysis, banks should only slot the principal of the bond to next call date or final maturity date when the option is deeply in-the-money or out-the-money, respectively.
If the first option is chosen, then the automatic embedded call option needs to be treated separately - just like caps/floors on a loan - either as a short/sold option (if the bond is an asset) or a long/bought option (if the bond is a liability). The FVAO (fair value of automatic option) should then be calculated in the baseline scenario as well as under stress scenarios, using a Black-76 approximation of a more advanced model like the HW1F model presented above. Under the standardized method the volatility also needs to be shocked by 25%.
At Finalyse, we have created an IRRBB solution, which calculates the end-to-end IRRBB calculations (including changes in FVAO values), which can be efficiently integrated into a bank’s existing internal risk systems.
FRTB treatment of Callable Bonds
Under the Basel III rules for Pillar 1 capital calculations (or variations thereof under local jurisdictions), market risk capital must be calculated in the trading book in accordance with the Fundamental Review of the Trading Book (FRTB) framework. FRTB will become applicable from Jan 2027 onwards in EU, but the requirement for reporting is already in force. The capital requirements are already in force in some other jurisdictions.
For the purpose of FRTB calculations, the trading instrument needs to be assigned to all relevant regulatory risk factors defined within each of the regulatory risk classes (interest rate risk, credit spread risk, foreign exchange risk, equity risk, commodity risk). The bank should calculate (delta, vega or curvature) sensitivities to every risk factors in scope, apply the regulatory risk weights and aggregate weighted sensitivities within and across all relevant buckets using the medium, high and low correlation levels defined in the regulation. This leads to the capital charge for the sensitivity-based method (SBM), which is also aggregated with the capital calculated in the Default Risk Charge and Residual Risk Add-on steps.
The table provides an overview of the calculation steps for the SBM component when the HW1F is used to price callable bonds:
Risk Class | Risk Factor – Delta | Risk Factor -Vega | Risk Factor - Curvature |
General Interest Rate Risk (GIRR)
| Delta sensitivity is calculated tenor by tenor by 1) “bumping” interest rates by 1 basis point for a specific tenor, 2) recalibrating the HW1F model and 3) repricing the callable bond price under the recalibrated model. Delta sensitivities are associated to the specific risk-free curve used for bond pricing. | Vega sensitivity to the implied volatility is calculated by 1) applying a 1% -absolute “bump” to all Black-Scholes implied volatilities used in the calibration, 2) recalibrating the HW1F model and 3) repricing the callable bond price under the recalibrated model. The resulting vega is then allocated across 2 dimensions: the option expiry and the remaining bond maturity at expiration. | Curvature sensitivity is calculated by applying up and down parallel shocks to the risk-free curve used for bond pricing and recalculating the callable bond price under the HW1F model. |
Credit Spread Risk non-securitization (CSR) | CSR delta sensitivity on fixed-rate bonds is calculated in the same way as GIRR delta sensitivity | Our HW1F modelling approach assumes that credit spreads are non-stochastic, resulting in the absence of any vega. Some banks decide to calculate curvature on credit spread curve as a secondary risk factor. Some (non-EU) regulators also explicitly require to calculate vega and curvature for both GIRR and CSR. | |
Foreign Exchange Risk (FX) | For bonds denominated in foreign currency, the FX delta exposure is equal to the value of the bond converted in the reporting currency. | Bonds do not display any vega or curvature sensitivity to the foreign exchange rate. | |
At Finalyse, we have created a Standardized Approach based FRTB calculator which performs the risk-weighting and aggregation of all FRTB sensitivities and generates the regulatory reports. Additionally, the FVS team in Finalyse has built-in models for calculating the sensitivities for all the different instrument types (ranging from simple products like bonds to complex products like range accruals and other American and Bermudian payoff derivatives). For an efficient calculation of the sensitivities for large portfolios, the sensitivities are computed using automatic adjoint differentiation (AAD) technique rather than with a finite difference method. These calculations can be implemented within a bank’s internal systems or can be accessed via our APIs.
Conclusion
In this post, we highlighted key aspects of interest-rate modelling and the complexity involved in pricing and calculating sensitivities for callable bonds. Finalyse has extensive expertise across the full spectrum of market-risk calculations—from model development and validation to the implementation of regulatory requirements such as IRRBB and FRTB. We also provide independent valuation services for OTC vanilla and exotic products.
Bibliography
1. Oprea, A. The Use of Principal Component Analysis (PCA) in Building Yield Curve Scenarios and Identifying Relative-Value Trading Opportunities on the Romanian Government Bond Market. J. Risk Financial Manag. 2022, 15, 247. doi.org/10.3390/jrfm15060247
Finalyse InsuranceFinalyse offers specialized consulting for insurance and pension sectors, focusing on risk management, actuarial modeling, and regulatory compliance. Their services include Solvency II support, IFRS 17 implementation, and climate risk assessments, ensuring robust frameworks and regulatory alignment for institutions. |

Our Insurance Services
Check out Finalyse Insurance services list that could help your business.
Our Insurance Leaders
Get to know the people behind our services, feel free to ask them any questions.
Client Cases
Read Finalyse client cases regarding our insurance service offer.
Insurance blog articles
Read Finalyse blog articles regarding our insurance service offer.
Trending Services
BMA Regulations
Designed to meet regulatory and strategic requirements of the Actuarial and Risk department
Solvency II
Designed to meet regulatory and strategic requirements of the Actuarial and Risk department.
Outsourced Function Services
Designed to provide cost-efficient and independent assurance to insurance and reinsurance undertakings
Finalyse BankingFinalyse leverages 35+ years of banking expertise to guide you through regulatory challenges with tailored risk solutions. |

Trending Services
AI Fairness Assessment
Designed to help your Risk Management (Validation/AI Team) department in complying with EU AI Act regulatory requirements
CRR3 Validation Toolkit
A tool for banks to validate the implementation of RWA calculations and be better prepared for CRR3 in 2025
FRTB
In 2025, FRTB will become the European norm for Pillar I market risk. Enhanced reporting requirements will also kick in at the start of the year. Are you on track?
Finalyse ValuationValuing complex products is both costly and demanding, requiring quality data, advanced models, and expert support. Finalyse Valuation Services are tailored to client needs, ensuring transparency and ongoing collaboration. Our experts analyse and reconcile counterparty prices to explain and document any differences. |

Trending Services
Independent valuation of OTC and structured products
Helping clients to reconcile price disputes
Value at Risk (VaR) Calculation Service
Save time reviewing the reports instead of producing them yourself
EMIR and SFTR Reporting Services
Helping institutions to cope with reporting-related requirements
CONSENSUS DATA
Be confident about your derivative values with holistic market data at hand
Finalyse PublicationsDiscover Finalyse writings, written for you by our experienced consultants, read whitepapers, our RegBrief and blog articles to stay ahead of the trends in the Banking, Insurance and Managed Services world |

Blog
Finalyse’s take on risk-mitigation techniques and the regulatory requirements that they address
Regulatory Brief
A regularly updated catalogue of key financial policy changes, focusing on risk management, reporting, governance, accounting, and trading
Materials
Read Finalyse whitepapers and research materials on trending subjects
Latest Blog Articles
Contents of a Recovery Plan: What European Insurers Can Learn From the Irish Experience (Part 2 of 2)
Contents of a Recovery Plan: What European Insurers Can Learn From the Irish Experience (Part 1 of 2)
Rethinking 'Risk-Free': Managing the Hidden Risks in Long- and Short-Term Insurance Liabilities
About FinalyseOur aim is to support our clients incorporating changes and innovations in valuation, risk and compliance. We share the ambition to contribute to a sustainable and resilient financial system. Facing these extraordinary challenges is what drives us every day. |

Finalyse CareersUnlock your potential with Finalyse: as risk management pioneers with over 35 years of experience, we provide advisory services and empower clients in making informed decisions. Our mission is to support them in adapting to changes and innovations, contributing to a sustainable and resilient financial system. |

Our Team
Get to know our diverse and multicultural teams, committed to bring new ideas
Why Finalyse
We combine growing fintech expertise, ownership, and a passion for tailored solutions to make a real impact
Career Path
Discover our three business lines and the expert teams delivering smart, reliable support



