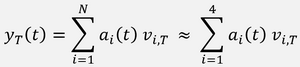Non-Maturity Deposit Modelling

Written by Augustin de Maere, Managing Consultant

Non-maturity deposits are liabilities that are characterized by two key features: the interest-rate paid on the liability is set up unilaterally by the Bank, and customer is free to withdraw the funds at any point in time. The contractual maturity is therefore overnight, but in practice, these liabilities are known to exhibit a significant stickiness, and most have a significant effective duration.  

The behaviour of the balances may be modelled under three different regimes: in run-off, in a static balance-sheet and assuming inflows of new clients. The treatment of non-maturity deposits is therefore at the edge between liquidity management and asset & liability management. It is important for banks to properly capture these features, because it will result in a more accurate assessment of their liquidity needs and interest-rate sensitivities. It will also play a crucial role in the transfer pricing of deposits, the interest-rate risk in the banking book calculations (IRRBB) and the internal liquidity adequacy assessment process (ILAAP).

The factors affecting non-maturity deposits can be classified in three different types:

• Market factors: the prevailing rates on the market (interbank and governments) 
• Macro-economic factors:  inflation, economic growth, …
• Behavioural factors: the reaction of the customer to the environment.

Modelling non-maturity deposits consists in correctly capturing the relationship between the client rate and balances with the prevailing market rates. The prevailing market rates are usually swap rates, government bond rates or central bank interest rates. These rates are assumed to reflect the risk-free yield a bank may expect from its assets.

Three levels of models are therefore required, as illustrated in Figure 1. A first model will capture the evolution of market rates. A second model will forecast the evolution of the deposit rates conditional on these market rates. Finally, a third model will provide the change in volumes. The next sections will provide more insights in the modelling requirements and the most common difficulties encountered in the development of these models.

Market models are usually pricing models, such as the 2-factor Cox-Ingersoll-Ross model (CIR2++) or the Libor Market Model (LMM). These models are usually calibrated on the current interest rate swap curve and a volatility surface from interest rate derivatives (e.g. swaptions). Some important properties of these models that the bank should be aware are highlighted in Figure 2. 

With statistical models, the aim is to forecast the future volatility of interest rates based on the past. The simplest approach is to apply a vector autoregressive (VAR) model to the principal components of the yield curve, but more advanced approaches may also be considered, e.g. by incorporating econometric expertise and linking the projections to macro-economic factors or by using machine learning models such as long short-term memory (LTSM) neural networks.

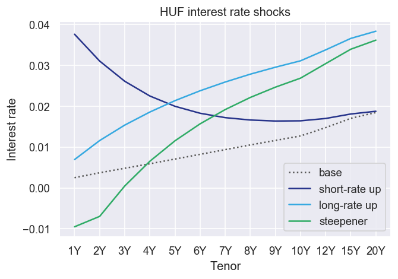
Finally, the evolution of the market rates is sometimes simply directly provided by the Bank or by the regulator. For instance, the European Banking Authority (EBA) prescribes specific interest rate shocks in its most recent Interest Rate Risk in the Banking Book guidelines (IRRBB).  Some of these shocks are reported in Figure 3.

What is Principal Component Analysis?

Principal Component Analysis is a dimensionality reduction technique, which aims at transforming a set of correlated observations into uncorrelated variables. If y_T (t) denote the tenor T of the swap curve at time t, then the curve can be decomposed as a sum of basic curves v_(i,T)  called principal components:

In the case of yield curve modelling, two other side benefits of PCA arise:

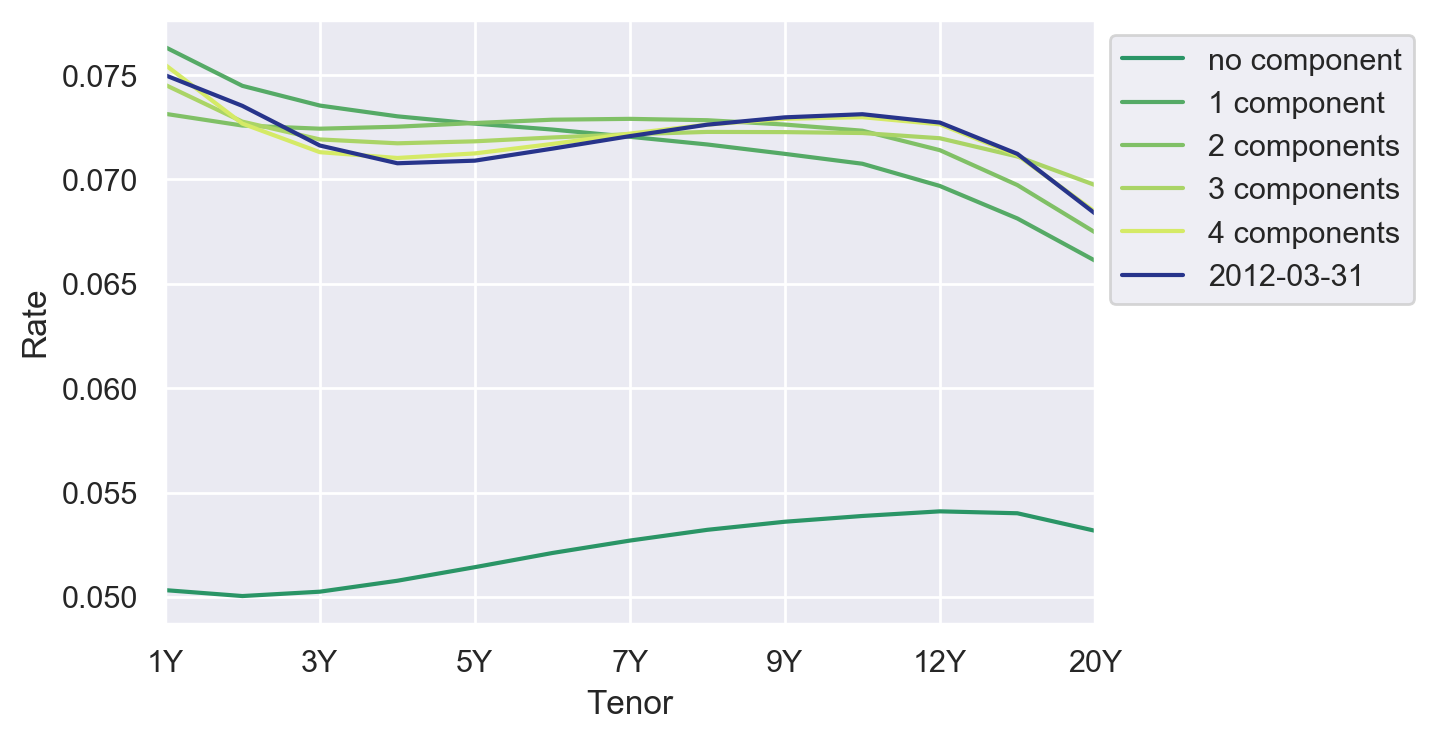
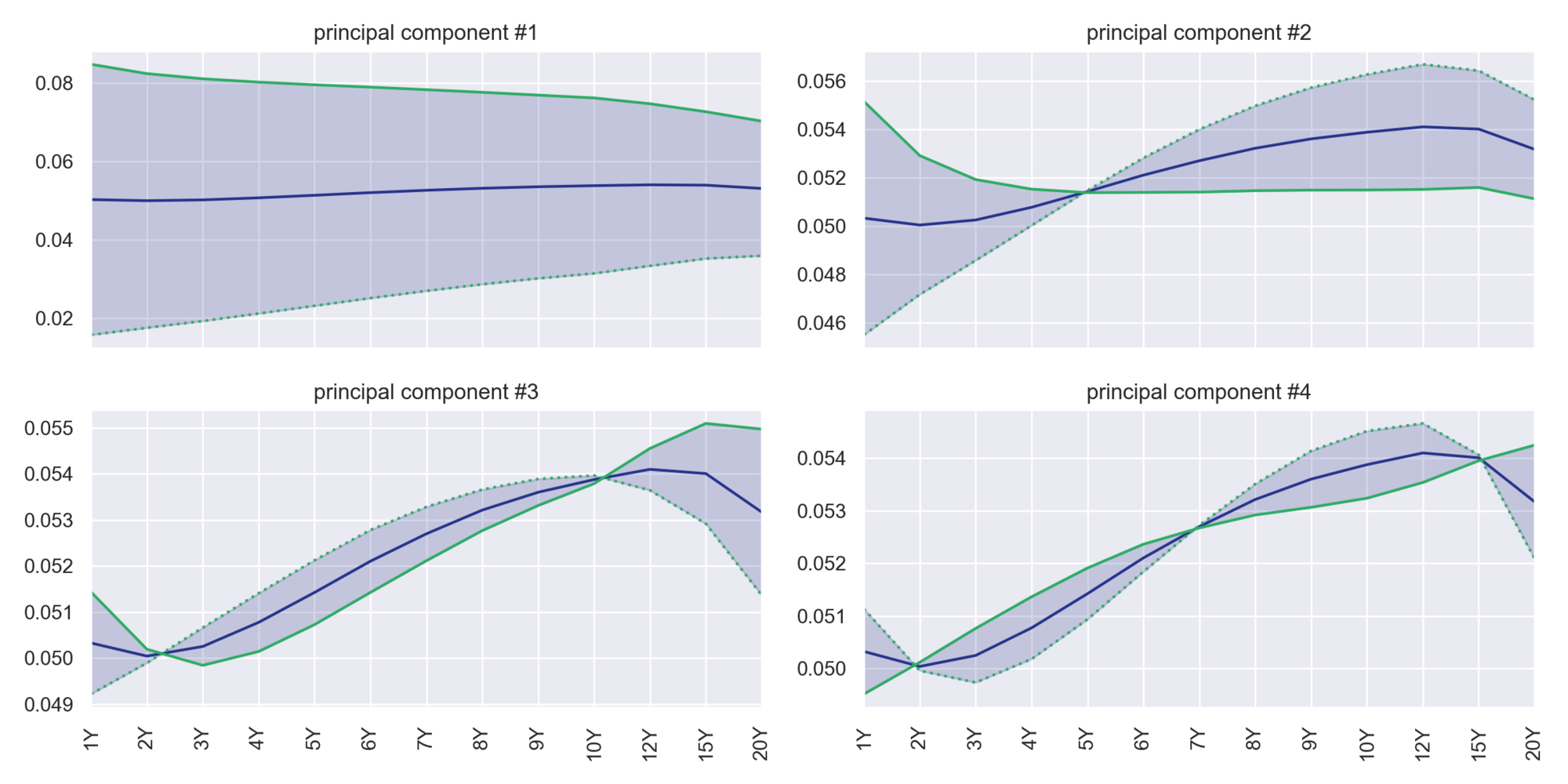
• The three first principal components have an interesting financial interpretation in term of level, slope and curvature of the yield curve respectively, as can be seen in Figure 6, where 1 standard deviation shocks are applied to each principal component. The fourth component has no direct interpretation and corresponds to more complicated but less significant changes in the shape of the yield curve.
• Only the first principal factor loading – the level  a_1 (t) - has a unit-root. Other principal factors are stationary.

Like market rates, both time series also appear to have a unit-root, and specific regression techniques have therefore to be used. The most standard technique for unit-root process are ARIMA process: the time series is first differentiated until it becomes stationary and is then regressed against stationary exogenous variables Xt. For the deposit rate r_t, themodel formulation could be:

Δr_t=α Δr_t-1+β X_t +γ+ ϵ_t

In the above equation, the exogenous variables are stationary, which implies that each variable must be differentiated until it becomes stationary. While this formulation is extremely flexible and provides excellent one-step ahead projections, its long-term stability may be deteriorated, because it does not include the fact that there is a long-term equilibrium between the deposit rates and the market rates. This long-term equilibrium is captured in a cointegration relationship: while deposit rates and market rates may have a unit-root, there is a linear combination of these variables that is stationary, and this combination can be exploited in an Error Correction Model (ECM). If X_t^(ex) and X_t^(co) are respectively the stationary and non-stationary exogenous variables, the deposit rate is modelled as:

Δr_t=α(r_t-1-η X_t-1^co)+ D X_t^ex+γ+ ϵ_t

The term in parenthesis represent the long-term trend for the deposit rate r_^t. Assuming that α<0, the process will tend to converge exponentially fast toward the long-term equilibrium value of η X_(t-1)^(co) (a). However, the short-term dynamic will be perturbed by shocks arising from other stationary short-term variables in D X_t^(ex) and from the other unexplained factors ϵ_t. 

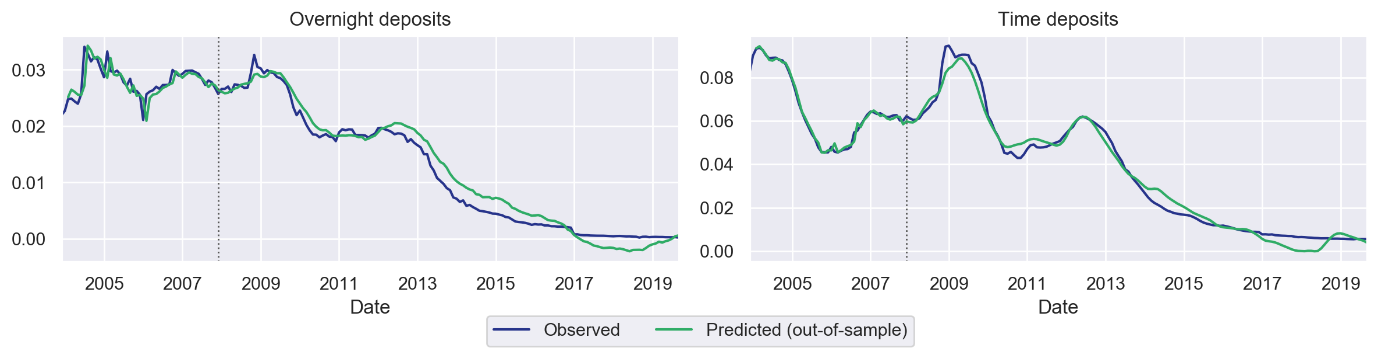
As an illustration, two models of the national average of deposit rates for overnight and time deposits were calibrated using the error correction model formulation. The models were assessed not only for their one-step ahead statistical properties (Bayesian Information Criterion, t-tests on significance, ADF and KPSS tests for stationarity, Ljung-Box tests for autocorrelation of the residuals, …)  but also for their economic soundness and the quality of their out-of-sample predictions (starting from December 2007). In an out-of-sample prediction, the predictions of the model at a given time step are given as input for the forecast of the next time step, and so on, therefore ensuring that the evolution of the model is significantly driven by the exogenous factors, and not only by its auto-regressive properties. 

The models are therefore not only able to perform accurate projections on the short-term, but also on the long-term. Curiously enough, the best models were based on swap rates for overnight rates, and on government rates for time deposits. For overnight deposit, the quality of the fit is slightly deteriorated from 2013 onwards, but model performance may be improved by properly handling the legal floor of the deposit rate (using a censored regression), and by introducing an asymmetry in the adjustments of the rates (banks are usually faster to reflect decrease in rates to their customer than the opposite). Incorporating information from yield curve of other currencies may also be useful, especially if foreign-currency deposits are used e.g. as a protection against inflation. The key attention points are summarized in Figure 8.

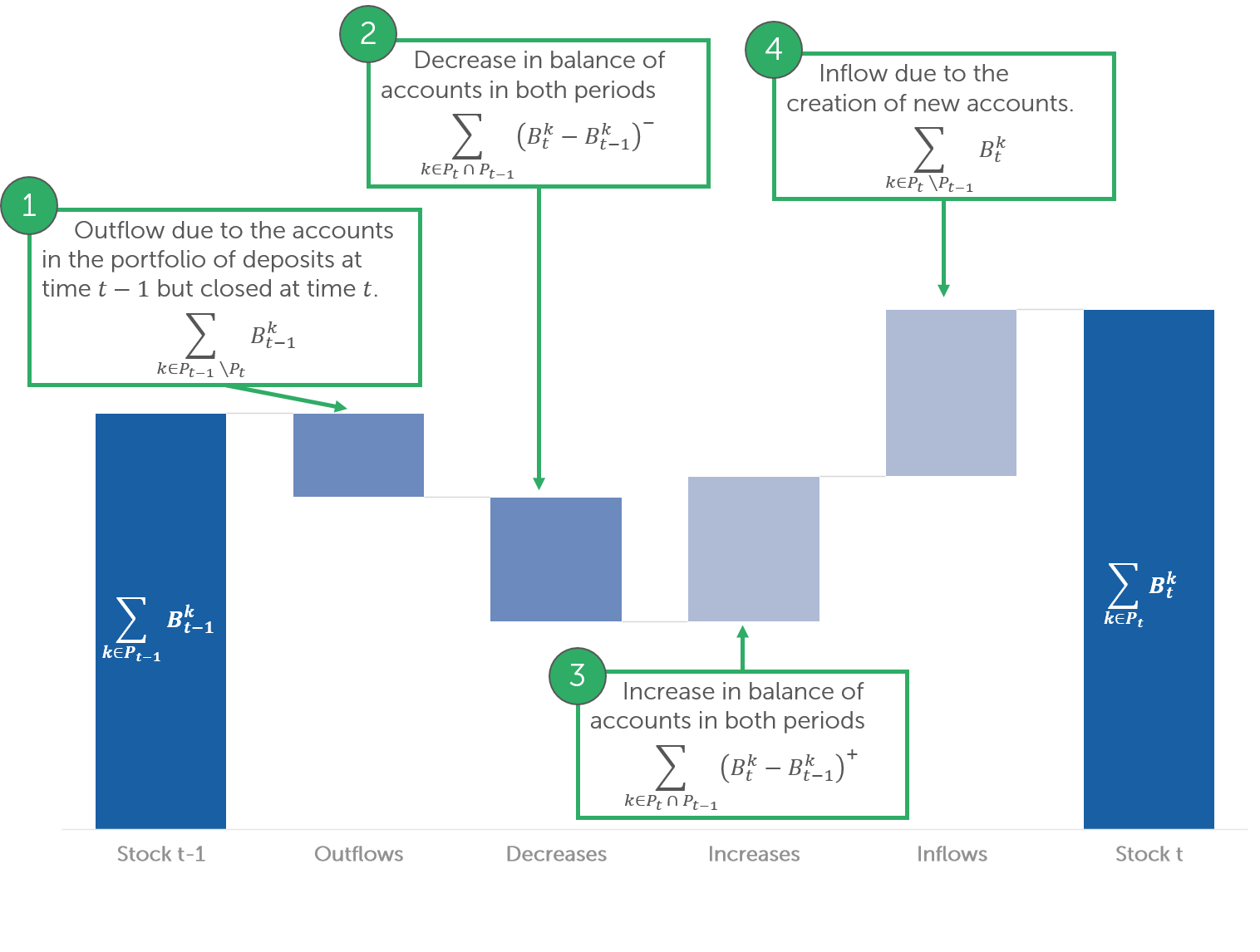
Volume modelling is probably the most complicated part of NMD modelling, and the most demanding in term of data. Let us assume that B_t^k  is the balance of account k at time t  and that snapshots of balances of accounts are available at a given unit frequency. Then, the evolution of the volumes can be broken down in four components:

• outflows of accounts, deactivated or closed accounts over the period
• decrease in balances, on accounts existing at the beginning and end of the period;
• increase in balances, on accounts existing at the beginning and end of the period,
• inflows of accounts: new accounts opened. 

Each term can then be modelled using specific and tailored formulations. For instance, inflows are typically provided using assumptions from the budget plan. On the other side, outflows may be derived using hazard rate models, and increases and decreases using classical time series methods. In the process, it is still possible to separate the core balances which are likely to be unaffected by change in rates. It is also advised to perform the modelling at product level, since transactional and non-transactional accounts will have a very different behaviour. The set of explanatory variables may be extended to include customer information (e.g. age, behaviour), macro-economic factors such as the inflation, and even features of agent-like models (such as the difference in return between different investment opportunities). The models are nevertheless likely to differ significantly from one institution to the other, because the amount of deposits is largely driven by behavioural factors.

Finally, it should be noted that the distinction between the different components in the deposit flows depends on two hidden assumptions:

• The level at which the accounts are aggregated. If the aggregation (the parameter k) is performed at the customer level, transfers between different accounts of the same customer will not appear in increases and decreases.
• The frequency at which the balances are recorded. For retail sight deposits, a daily frequency is likely to provide a totally different split than a monthly frequency.

Different model formulations are also possible. For instance, using ECM has the advantage of introducing a target deposit level that each customer will try to achieve. This feature is interesting for transactional accounts and savings account, since clients tend to keep a fixed safety buffer on their overnight accounts and to invest the excess money in more lucrative financial instruments (e.g. stocks, bonds, funds, etc.). Otherwise, a seasonally adjusted ARIMA model may provide a more general framework. 

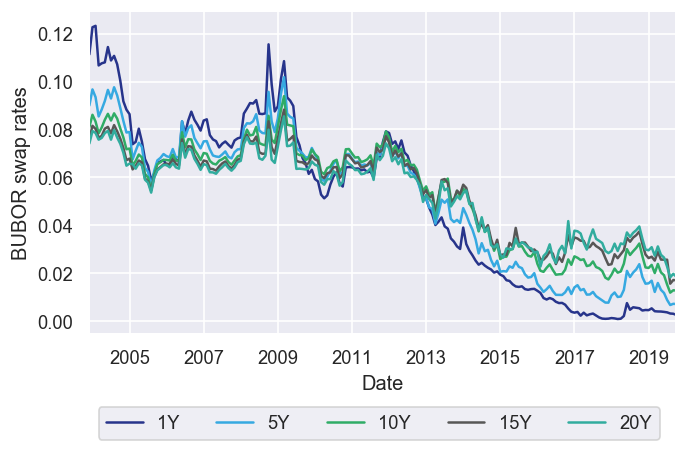
In order to illustrate the type of problems one can face in volume modelling, we designed a model for the total amount of overnight and time deposits in Hungary, retrieved from the statistical data warehouse of the MNB¹. A key feature of these time series is the apparent outflow from time deposits to overnight deposits taking place from 2013 onwards. In order to capture it, the following explanatory variables were included in the model:

• Principal components of the market swap and government curves
• Consumer Price Index, in order to work with constant prices. The drawback of including inflation is that it now needs to be forecasted conditional on the market interest rate scenario, which requires another econometric model.
• The difference between the client rate paid on time deposits and overnight deposits. Indeed, the outflow of time deposit is strongly correlated to a tightening of the spread between these two rates. When the premium paid on time deposits drops below 2%, volumes begin to decrease. The effect is non-linear, so the variable is transformed using a stepwise linear transformation.
• A dummy variable for the month of December, to account for year-end premiums.

¹. Hungarian Central Bank

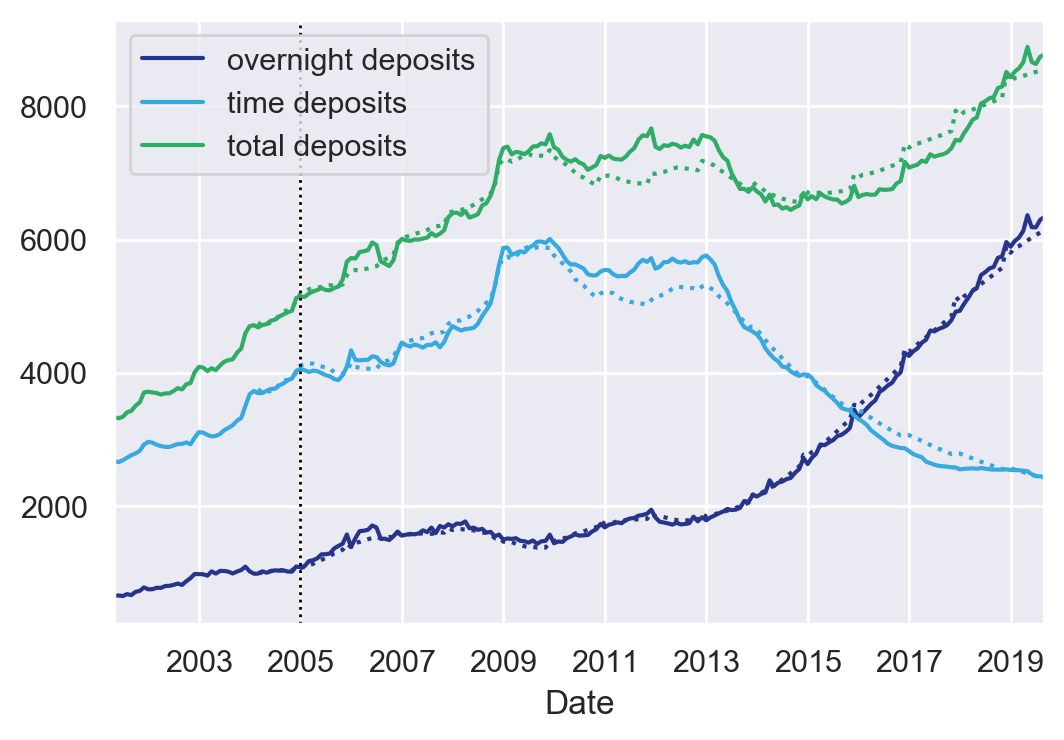
A vector error correction model was retained, whose results are reported in Figure 10 (dotted lines are out of sample predictions starting from 2005 onwards). The model perfectly captures the increase in in time deposits in end 2008, and the flows between the different type of deposits from 2013 onwards.

In the case of the deposits of a single institution, the behavioural effects are likely to be more significant that what was observed in this example, which may require creative modelling. It is therefore important to have a proper business understanding of the portfolio and to use expert assumptions when necessary. The main attention points for volume modelling are therefore summarized in Figure 11.

In the current low-interest rate environment, the modelling of non-maturity deposits has attracted interests from Banks. These models are used for critical purposes in banks such as the management of the interest rate risk of the balance sheet, or in their earnings, as it is now also expected from supervisory authorities. Finally, they are also used to determine of a transfer price for deposits, in order to retribute the business lines in charge of collecting the deposits appropriately.