By François-Xavier Duqué, Managing Consultant
and Marc-Louis Schmitz, Partner Valuation Services
Introduction
Since February 2017, the big players have been subject to the obligation of exchanging initial margin (IM) on non-cleared derivatives, while other players will see these IM obligations phased in for them over the next 4 years. In this article, we take a step back to reflect on this important evolution. We discuss the merits of an industry initiative to develop a standard initial margin model (ISDA SIMM) and the extent to which it echoes the Sensitivity Based FRTB Standard Approach.
The European Market Infrastructure Regulation, better known under its EMIR acronym, aims at reducing systemic risk arising from OTC derivatives. The regulation walks on three legs, each materialized by a set of Regulatory Technical Standards (RTS): Reporting, Clearing and Risk Mitigation. Variation Margin (VM) and Initial Margin (IM) are at the core of the Risk Mitigation effort.
While VM covers current exposure, IM is about the potential exposure that could arise following the default of a counterparty – and hence the last VM call – before the contracts can be replaced on the market.
More specifically, under EMIR, exchanging IM should protect both sides to an OTC derivative against a slippage of the MTM during a 10-day margin period of risk (MPoR) with a confidence interval of 99%. Putting a number on such a metric is challenging. The EMIR roadmap presents two paths: either use a standardized schedule-based approach or implement an internal margin model approved by supervisory authorities.
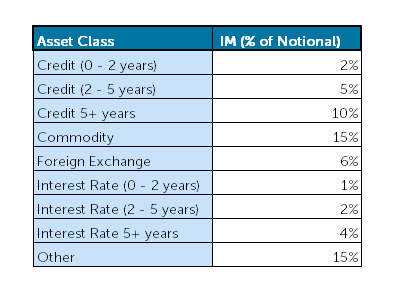
Scheduled-based method vs internal models
The scheduled-based method has the advantage of simplicity. Contract notionals are weighted individually according to their asset class (see table below) and added up. Some offset is allowed by applying the familiar net-to-gross ratio (NGR) to the resulting total. However, calculating IM under schedule-based method proves to be too costly in capital for many market participants. (The NGR is the ratio of the sum of positive and negative MTMs in the netting set (floored at zero) divided by the sum of positive MTMs in the netting set. Hence, the bigger the offset in MTMs, the lower the NGR).
Internal models can reduce the cost of posting collateral on IM significantly by considering all deal features and allowing for less-crude diversification effects. As for VaR and CVA, there are a number of modelling options, extending from parametric models to Monte Carlo stochastic diffusion, not forgetting historic simulation, which is a popular choice among clearers (LCH, CME, Eurex. etc.). Internal models however come with the burden of model governance (model development, validation, approval & maintenance). Besides, market participants are left exposed to the practical issue of managing collateral disputes: checking the correctness of the margin call a participant receives, ideally requires the participant to develop the same IM models developed by all its counterparties. So, a situation where a multitude of models coexist implies a huge operational complexity, arguably threatening the ability to comply with the regulation.
ISDA SIMM
Understandably, the industry initiative led by ISDA to develop a proprietary standard initial margin model (SIMM) has created a great deal of interest among market participants. The ISDA SIMM aims at striking a balance between conflicting objectives: non-procyclicality, ease of replication, transparency, calculation speed, cost, extensibility to new risk, predictable capital allocation, and, last but not least, being an appropriate measure of the risk involved. Next to these desirable features, participants using the SIMM model for each other’s margin calls benefit from more transparent dispute resolution. They also find relief on the governance front, as the ISDA owns the responsibility of maintaining the model, for example by performing an annual calibration of the model parameters. The model consists in a relatively simple three-step calculation:
- Firstly, risk sensitivities (“greeks”) are allocated across different product classes, risk classes, risk factors and risk buckets.
- Secondly, risk weights representing a 1-in-a-100 10-day market stress are applied.
- Thirdly, weighted sensitivities are aggregated via a sequence of nested correlation matrices.
What to expect?
Applying the ISDA SIMM model might potentially decrease the initial margin requirements by 5 compared o the schedule-based method. The significant advantage of the SIMM model lies in the possibility to 1) offset sensitivities of different deals within risk classes and 2) account for diversification across risk classes (via the use of correlations in the aggregation) within each product class.
However, the advantages of the SIMM model over a schedule-based approach are not indisputable. If trades are long-dated, always in the same direction or denominated in high volatility currencies, then the schedule-based methodology may be the simplest and most efficient solution.
The advantage of the SIMM model over internal models is real but comes with a caveat. Sensitivities are not easy to calculate; different models will produce different sensitivities. Because ISDA SIMM does not cover this aspect, it will not eliminate all collateral disputes. But the existence of shared and standardized templates for sensitivities will facilitate the reconciliation of discrepancies.
Akin to FRTB SA?
ISDA SIMM shares many similarities with the Sensitivity Based Approach in the FRTB Standard Approach. Both SIMM and FRTB aggregate weighted sensitivities by using a sequence of nested correlation matrices.
As popular wisdom goes, the devil is in the details. Below is a list of points illustrating that SIMM and FRTB are “similar but somehow different”:
- SIMM and FRTB share 4 risk classes (IR, FX, EQ, CO), but credit is split across 2 risk classes in SIMM (qualifying versus non-qualifying) versus 3 risk classes in FRTB (non-securitisation, securitisation, correlation trading).
- Both rely on delta and vega sensitivities. However, SIMM computes curvature as a transformation of vega, while FRTB requires an additional sensitivity to be calculated.
- SIMM does not allow offset between sensitivities in the same risk class across different product classes (e.g. DV01 of an IRS does not offset the DV01 of a CDS).
- SIMM has two additional interest rate buckets (1W, 1M).
- Weights and correlations are obviously different (calibration for capital versus margining).
- Unlike SIMM, FRTB calculates the risk charge with three sets of correlation (high, medium, low) and takes the largest of these.
- Unlike FRTB, SIMM uses concentration thresholds to account for concentration risk.
Still, the analogy between ISDA SIMM and FRTB contributes to the appeal of the ISAD SIMM approach. Overlapping of SIMM and FRTB requirements may minimise implementation costs significantly and allow banks to benefit from a systematic approach to risk management.
Finalyse InsuranceFinalyse offers specialized consulting for insurance and pension sectors, focusing on risk management, actuarial modeling, and regulatory compliance. Their services include Solvency II support, IFRS 17 implementation, and climate risk assessments, ensuring robust frameworks and regulatory alignment for institutions. |

Our Insurance Services
Check out Finalyse Insurance services list that could help your business.
Our Insurance Leaders
Get to know the people behind our services, feel free to ask them any questions.
Client Cases
Read Finalyse client cases regarding our insurance service offer.
Insurance blog articles
Read Finalyse blog articles regarding our insurance service offer.
Trending Services
BMA Regulations
Designed to meet regulatory and strategic requirements of the Actuarial and Risk department
Solvency II
Designed to meet regulatory and strategic requirements of the Actuarial and Risk department.
Outsourced Function Services
Designed to provide cost-efficient and independent assurance to insurance and reinsurance undertakings
Finalyse BankingFinalyse leverages 35+ years of banking expertise to guide you through regulatory challenges with tailored risk solutions. |

Trending Services
AI Fairness Assessment
Designed to help your Risk Management (Validation/AI Team) department in complying with EU AI Act regulatory requirements
CRR3 Validation Toolkit
A tool for banks to validate the implementation of RWA calculations and be better prepared for CRR3 in 2025
FRTB
In 2025, FRTB will become the European norm for Pillar I market risk. Enhanced reporting requirements will also kick in at the start of the year. Are you on track?
Finalyse ValuationValuing complex products is both costly and demanding, requiring quality data, advanced models, and expert support. Finalyse Valuation Services are tailored to client needs, ensuring transparency and ongoing collaboration. Our experts analyse and reconcile counterparty prices to explain and document any differences. |

Trending Services
Independent valuation of OTC and structured products
Helping clients to reconcile price disputes
Value at Risk (VaR) Calculation Service
Save time reviewing the reports instead of producing them yourself
EMIR and SFTR Reporting Services
Helping institutions to cope with reporting-related requirements
CONSENSUS DATA
Be confident about your derivative values with holistic market data at hand
Finalyse PublicationsDiscover Finalyse writings, written for you by our experienced consultants, read whitepapers, our RegBrief and blog articles to stay ahead of the trends in the Banking, Insurance and Managed Services world |

Blog
Finalyse’s take on risk-mitigation techniques and the regulatory requirements that they address
Regulatory Brief
A regularly updated catalogue of key financial policy changes, focusing on risk management, reporting, governance, accounting, and trading
Materials
Read Finalyse whitepapers and research materials on trending subjects
Latest Blog Articles
Contents of a Recovery Plan: What European Insurers Can Learn From the Irish Experience (Part 2 of 2)
Contents of a Recovery Plan: What European Insurers Can Learn From the Irish Experience (Part 1 of 2)
Rethinking 'Risk-Free': Managing the Hidden Risks in Long- and Short-Term Insurance Liabilities
About FinalyseOur aim is to support our clients incorporating changes and innovations in valuation, risk and compliance. We share the ambition to contribute to a sustainable and resilient financial system. Facing these extraordinary challenges is what drives us every day. |

Finalyse CareersUnlock your potential with Finalyse: as risk management pioneers with over 35 years of experience, we provide advisory services and empower clients in making informed decisions. Our mission is to support them in adapting to changes and innovations, contributing to a sustainable and resilient financial system. |

Our Team
Get to know our diverse and multicultural teams, committed to bring new ideas
Why Finalyse
We combine growing fintech expertise, ownership, and a passion for tailored solutions to make a real impact
Career Path
Discover our three business lines and the expert teams delivering smart, reliable support


